wx-wow(微信小程序动效库)
阅读更多
 wx-wow(微信小程序动效库)
wx-wow(微信小程序动效库)
 蓝桥杯真题测试次数(详解)
蓝桥杯真题测试次数(详解)
 Java版五子棋小游戏(java控制台)
Java版五子棋小游戏(java控制台)
 综合程序设计导弹追踪问题(matlab)
综合程序设计导弹追踪问题(matlab)
 蓝桥杯历届真题高僧斗法(博弈-Nim博弈)
蓝桥杯历届真题高僧斗法(博弈-Nim博弈)
 一款酷炫的动态背景
一款酷炫的动态背景
 汉诺塔游戏(递归与非递归详解)
汉诺塔游戏(递归与非递归详解)
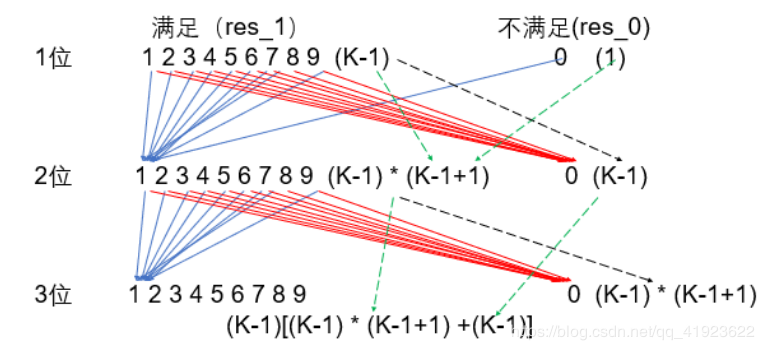 K-进制数
K-进制数
