蓝桥杯 历届试题 对局匹配
问题描述 小明喜欢在一个围棋网站上找别人在线对弈。这个网站上所有注册用户都有一个积分,代表他的围棋水平。
小明发现网站的自动对局系统在匹配对手时,只会将积分差恰好是K的两名用户匹配在一起。 如果两人分差小于或大于K,系统都不会将他们匹配。
现在小明知道这个网站总共有N名用户,以及他们的积分分别是A1, A2, … AN。
小明想了解最多可能有多少名用户同时在线寻找对手,但是系统却一场对局都匹配不起来 (任意两名用户积分差不等于K)? 输入格式
第一行包含两个个整数N和K。 第二行包含N个整数A1, A2, … AN。对于30%的数据,1 <= N <= 10 对于100%的数据,1 <= N <= 100000, 0 <= Ai <=
100000, 0 <= K <= 100000 输出格式 一个整数,代表答案。 样例输入 10 0 1 4 2 8 5 7 1 4 2
8 样例输出 6
题目链接:C语言网: http://www.dotcpp.com/oj/problem1842.html
蓝桥杯: http://lx.lanqiao.cn/problem.page?gpid=T454
如果 用户积分之间相互有冲突 要想最多人 则需 每隔k积分的用户在线如下图
假设每个 积分段的用户 都一样的话 则要么取蓝色积分的用户 要么取红色用户都行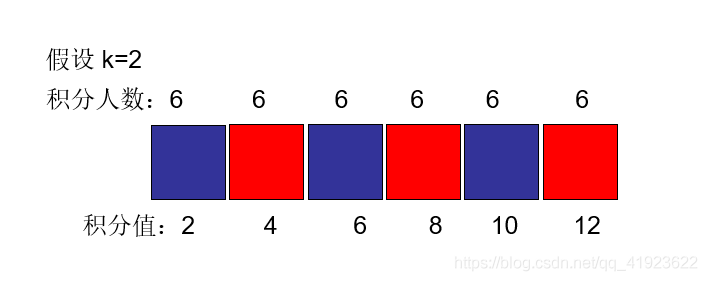
但是如果 积分人数如下图 肯定 每隔一个取得办法就不行了 正解 应该是看下面吧
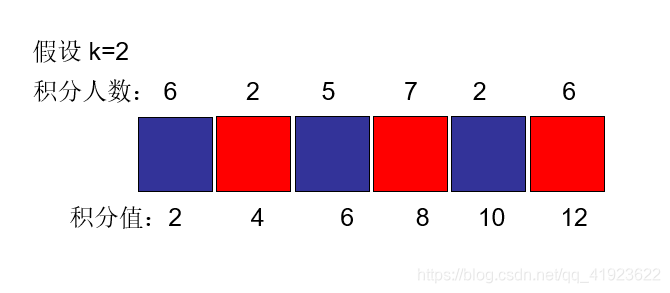
正解:取红色部分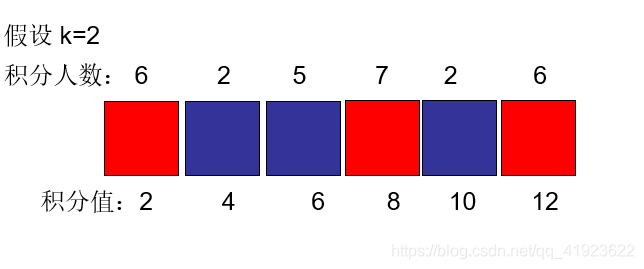
人眼看一眼就知道了 计算机 则需要动态规划的方式来到达目的 下面是该题的核心(理论就不讲了 讲讲具体实现 体会动态更新的过程)
从冲突用户第3个用户开始 那么他只能与他前前用户可以同时在线
所以 dp[6]=dp[2]+5=11 (dp[i]=k 代表 从第1个积分的用户到积分为i的用户 可同时在线的最大人数)
然后 更新一下 他 前面一个积分用户的dp[i-k]的值,为他后面一个积分的用户做准备 dp[i-k]=Max(dp[i-k],dp[i-2*k]);
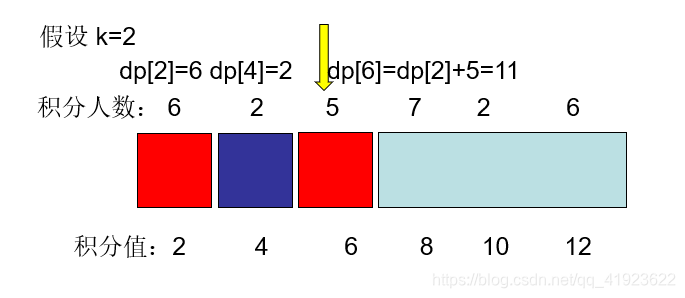
更新dp[i-k] 这个时候dp[i-k]=dp[4]=2就替换dp[i-2*k]=dp[2]=6 实质就是隔了2k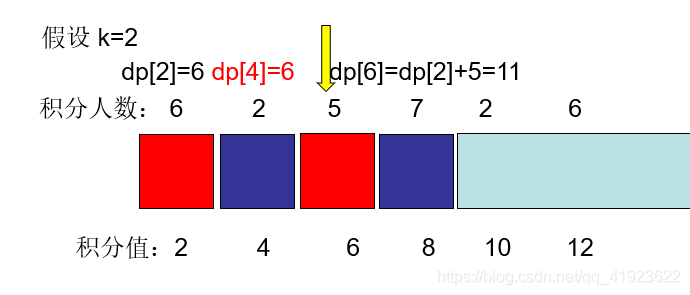
当处理第4个积分用户的 dp[8] 只需找他前前一个积分用户
然后更新他前一个 积分的用户 但是dp[i-k]>dp[i-2*k] 所以无需更新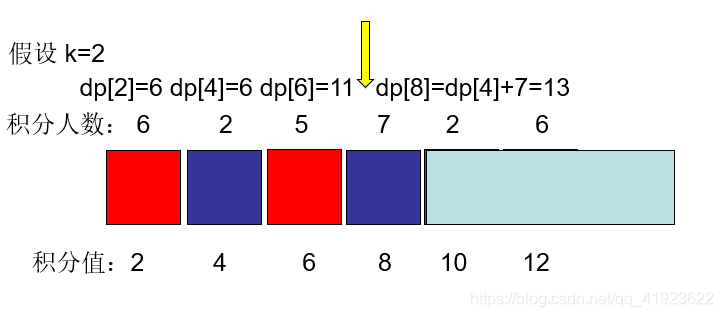
。。。。。
更新 到最后一个积分用户 就可以 得出当 积分为 2 4 6 8 10 12 这组相互冲突的用户之间 最大的可同时在线人数了
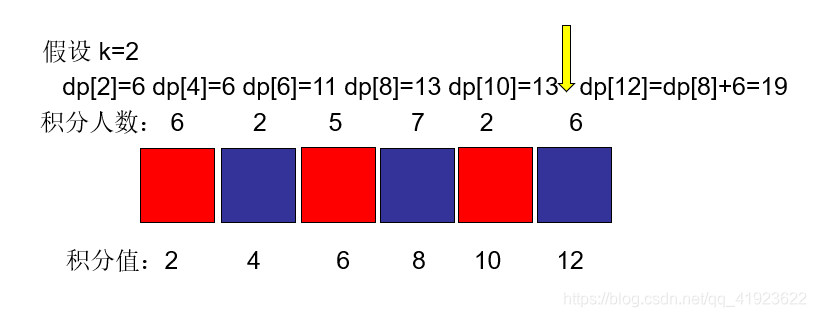
综上 :
就可以得出
dp[i]=jf[i]+dp[i-2k];//从第1个积分用户到当前积分的最大人数
dp[i-k]=Max(dp[i-k],dp[i-2k]);//更新当前上一个积分用户
当然 也可以优化一下空间复杂度
用 dp替换dp[i] qq_dp替换dp[i-2*k] q_dp替换dp[i-k]
节省掉dp 开的空间
写为
qq_dp=jf[ks]; q_dp=jf[ks+k];
for(i=ks+2*k;i<=js;i=i+k)
{
dp=jf[i]+qq_dp;
//更新从第一到当前最大 积分只要至少隔一个k就行了 所以 本积分人数加上比他小两个k积分的用户人数
q_dp=Max(q_dp,qq_dp);//更新前一个k积分用户
qq_dp=q_dp; q_dp=dp;
}
AC代码:
#include <stdio.h>
#include <string.h>
long int jf[100012]={0};//jf[i]=k 代表积分为i的用户 有k个人
long int n,k;
long int Max(long int a,long int b ) { if(a>b)return a;else return b;}
long int f(long int ks,long int js)
{ long int i;
long int dp[100012];
memset(dp,0,sizeof(dp));
i=ks+2*k; dp[ks]=jf[ks];dp[ks+k]=jf[ks+k];//初始化 前 2个 连续
//i从相互冲突的第3个人开始 第一用户 第二用户
for(i=ks+2*k;i<=js;i=i+k)
{
dp[i]=jf[i]+dp[i-2*k];
//更新从第一到当前最大 积分只要至少隔一个k就行了 所以 本积分人数加上比他小两个k积分的用户人数
dp[i-k]=Max(dp[i-k],dp[i-2*k]);//更新前一个k积分用户
}
return Max(dp[i-k],dp[i-2*k]);
}
int main()
{long int i,sum=0,s,max=0,t;
scanf("%ld%ld",&n,&k);
for(i=1;i<=n;i++)
{ scanf("%ld",&s);
jf[s]++;if(max<s)max=s;
}
if(k==0){//为0的时候特殊处理 每个积分 只允许1个人
for(i=0;i<=max;i++)if(jf[i]!=0)sum++;
}else{
for(i=0;i<=max;i++)
{ if(jf[i]==0)continue;
t=1; while(jf[i+t*k]!=0)t++;//找出 有多少分数差k的用户(就是同时在线会冲突)
if(t!=1) sum+=f(i,i+(t-1)*k);//有冲突的人 的起始用户积分与结束用户积分
else sum+=jf[i];//该积分就一个人 就不存在冲突 加上就好
t=1; while(jf[i+t*k]!=0) {jf[i+t*k]=0;t++;}//找过了就清零
}
}
printf("%ld\n",sum);
return 0;
}
AC 代码2
#include <stdio.h>
#include <string.h>
int jf[100012]={0};//jf[i]=k 代表积分为i的用户 有k个人
int n,k;
int Max( int a, int b ) { if(a>b)return a;else return b;}
int f( int ks, int js)
{ int i;
int dp,q_dp,qq_dp;
qq_dp=jf[ks];q_dp=jf[ks+k];//初始化 前 2个 连续
//i从相互冲突的第3个人开始 第一用户 第二用户
for(i=ks+2*k;i<=js;i=i+k)
{
dp=jf[i]+qq_dp;
//更新从第一到当前最大 积分只要至少隔一个k就行了 所以 本积分人数加上比他小两个k积分的用户人数
q_dp=Max(q_dp,qq_dp);//更新前一个k积分用户
qq_dp=q_dp;q_dp=dp;
}
return Max(q_dp,qq_dp);
}
int main()
{int i,sum=0,s,max=0,t;
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++)
{ scanf("%d",&s);
jf[s]++;if(max<s)max=s;
}
if(k==0){
for(i=0;i<=max;i++)if(jf[i]!=0)sum++;
}else{
for(i=0;i<=max;i++)
{ if(jf[i]==0)continue;
t=1; while(jf[i+t*k]!=0)t++;//找出 有多少分数差k的用户(就是同时在线会冲突)
if(t!=1) sum+=f(i,i+(t-1)*k);//有冲突的人 的起始用户积分与结束用户积分
else sum+=jf[i];//该积分就一个人 就不存在冲突 加上就好
t=1; while(jf[i+t*k]!=0) {jf[i+t*k]=0;t++;}//找过了就清零
}
}
printf("%d\n",sum);
return 0;
}




